Trójkąt to najprościej rzecz ujmując, wielokąt o trzech bokach. Wyróżnić możemy kilka rodzajów trójkątów: ostrokątny – wówczas, gdy wszystkie kąty są ostre (od 0 stopni do 90 stopni), prostokątny – jeżeli ma jeden kąt prosty (90 stopni), rozwartokątny – jeżeli ma jeden kąt rozwarty (większy niż 90 stopni). Bez względu na to, o którym trójkącie mówimy, suma miar kątów wewnętrznych wynosi 180 stopni. Szczególne rodzaje trójkątów:
- Trójkąt równoramienny to nic innego, jak trójkąt o dwóch bokach równej długości,
- Trójkąt równoboczny to nic innego, jak trójkąt mający trzy boki równej długości.
- Trójkąt prostokątny jest trójkątem o kącie prostym pomiędzy dwoma bokami.
Na tym etapie warto byłoby przypomnieć, że pole trójkąta można obliczyć na wiele zróżnicowanych sposobów – w rzeczywistości wszystko zależy od tego, jakimi danymi dysponujemy. I tak najbardziej podstawowy wzór na pole trójkąta to:
P=1/2ah
gdzie:
P – pole trójkąta
a – długość boku trójkąta
h – wysokość trójkąta opuszczona na ten bok.
Wzór na pole trójkąta z sinusem
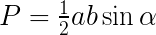
gdzie:
a, b to długości boków trójkąta
α to kąt pomiędzy bokami a i b.
Wzór na pole trójkąta wpisanego w okrąg
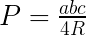
gdzie:
a, b, c to długości boków trójkąta
R to długość promienia okręgu opisanego na trójkącie
Wzór na pole trójkąta wpisanego w okrąg, gdzie podane są kąty
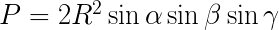
gdzie:
α, β, γ to kąty trójkąta
R to długość promienia okręgu opisanego na trójkącie
Wzór na pole trójkąta opisanego na okręgu
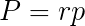
gdzie:
r to długość promienia okręgu wpisanego w trójkąt
p to połowa sumy długości wszystkich boków trójkąta (połowa obwodu trójkąta).
Trójkąt równoboczny
Przypomnijmy, że trójkąt równoboczny to trójkąt, który ma wszystkie boki tej samej długości, a jego kąty wewnętrzne są równe 60 stopni.
h = (a√3) : 2 – wysokość trójkąta równobocznego,
P = (a√3) : 4 – wzór na pole trójkąta równobocznego,
r = h : 3 – promień okręgu wpisanego w trójkąt równoboczny,
R = 2h : 3 – promień okręgu opisanego na trójkącie równobocznym.
Trójkąt prostokątny
Trójkąt prostokątny to trójkąt, którego jeden z kątów wewnętrznych jest prosty.
I tak:
Pole trójkąta prostokątnego o bokach a, b, c i wysokości h wyraża się następującymi wzorami:
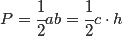
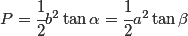
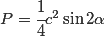
Własności trójkąta prostokątnego:
Promień okręgu wpisanego w trójkąt prostokątny:
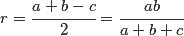
Promień okręgu opisanego na trójkącie prostokątnym