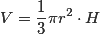Stożek to jedna z tych figur geometrycznych, która olbrzymiej ilości osób kojarzy się wyłącznie z czapeczkami urodzinowymi – i w tym skojarzeniu nie ma zupełnie nic niewłaściwego. Czapeczki wręczane np. gościom na przyjęciu urodzinowym mają kształt stożka. Na szczególną uwagę zasługuje również fakt, że stożek jest figurą niezwykle prostą i przyjemną do liczenia. Na początek warto byłoby więc nieco bliżej przyjrzeć się właściwościom stożka.
Własności stożka:
- przekrój osiowy to trójkąt,
- powstał przez obrót trójkąta,
- tworzącą stożka okreslana jest literą l,
- pole podstawy oblicza się ze wzoru na pole koła,
- objętość stożka oznaczana jest literą V.
Jak obliczyć pole całkowite stożka?
Liczenie pola stożka opiera się na dwóch głównych etapach – pierwszym jest przeliczenie pola podstawy stożka. Wzór na pole podstawy stożka jest tym samym, co wzór na pole koła, czyli P = π⋅r².
Kolejnym krokiem jest obliczyć pola powierzchni bocznej – w tym przypadku należy zastosować konkretny wzór. Tym sposobem możliwe będzie sprawne policzenie pola bocznego stożka. Pole boczne + pole podstawy stożka daje pole całkowite.
Wzór na pole boczne stożka:
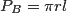
Wzór na pole podstawy stożka:

Wzór na pole całkowite stożka:

Jak obliczyć objętość stożka?
Liczenie objętość stożka może sprawiać wrażenie dość skomplikowanego zadania, ponieważ nie jest to do końca regularna figura. Stwierdzenie to nie jest jednak do końca prawdziwe. Kluczem do sukcesu okaże się skorzystanie z następującego wzoru:
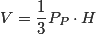
W przypadku stożka, gdzie w postawie będzie koło, mówimy o następującym wzorze: