Ciągiem geometrycznym nazywamy ciąg liczb, w którym każda kolejna liczba różni się od poprzedniej q razy. W praktyce oznaczać to będzie tylko tyle, że każdy wyraz ciagu – zaczynając od drugiego, powstał poprzez pomnożenie poprzedniego wyrazu przez pewną liczbę (wówczas wspomniane wcześniej q nazywane jest ilorazem ciągu). Ciąg geometryczny można opisać dzięki ogólnemu wzorowi tego ciągu.
Przykłady:
Ciąg (1,3,9,27,…)jest ciągiem geometrycznym o ilorazie 3,
Ciąg (-4,2,-1,½, -¼…) jest ciągiem geometrycznym o ilorazie – 1/2.
Ciąg (5,0,0,0,0,…) jest ciągiem geometrycznym o ilorazie 0.
Najważniejsze wzory na ciągu geometryczne:
Najważniejsze wzory dla ciągu geometrycznego
Najważniejsze wzory dla ciągu geometrycznego prezentują się następująco:
nty wyraz ciągu geometrycznego:
Suma ciągu geometrycznego:

Zależności między wyrazami ciągu geometrycznego:
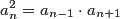
Przykład 1:
Wzór ogólny ciągu, którego pierwszy wyraz wynosi 3, a iloraz ciągu jest równy 4, prezentuje się następująco:
Z kolei wzór ogólny ciągu geometrycznego:
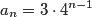
Własności ciągu geometrycznego:
Każdy wyraz ciągu geometrycznego spełnia warunek:

Gdy a1≠ 0, q=0, to ciąg geometryczny jest stały od wyrazu drugiego i ma postać: a1, 0, 0,…
- Ciąg geometryczny jest rosnący wówczas, gdy:
– dla a1 > 0, gdy q >1
– dla a1 < 0, gdy 0<q<1
- Ciąg geometryczny jest malejący wówczas, gdy:
– dla a1 > 0, gdy <0<q<1
– dla a1 < 0, gdy q > 1
- Ciąg geometryczny jest stały wówczas, gdy:
– dla a1 > 0, gdy q=1
– dla a1 < 0, gdy q=1.
- Ciąg geometryczny nie jest monotoniczny wówczas, gdy iloraz ciągu q < 0, ciąg jest naprzemienny i ma postać: a1, -a2, a3, -a4,…
- Jeżeli iloraz ciągu geometrycznego nie jest liczbą stałą – wówczas nie mówimy o ciągu geometrycznym.